Mi viejo Commodore 64, ¡cuántas horas de diversión que me diste!
Aquellos que se sientan nostálgicos podrán leer sobre la historia de los videojuegos en esta completa anotación: Historia de los Videojuegos.
miércoles, 30 abril, 2008
jueves, 27 marzo, 2008
¿Por qué son tan pequeños los átomos?
«Se han imaginado muchos ejemplos para familliarizar al público con esta idea, pero ninguno es más sorprendente que el empleado por Lord Kelvin: supongamos que pudiéramos marcar las moléculas de un vaso de agua; vertamos entonces el contenido del vaso en el océano y agitemos de forma que las moléculas marcadas se distribuyan uniformemente por los siete mares; si después llenamos un vaso de agua en cualquier parte del océano, encontraremos en él alrededor de un centenar de moléculas marcadas.»
Erwin Schrödingen en ¿Qué es la vida?, un libro divulgativo que además ha tenido una gran influencia en el desarrollo posterior de la biología.
miércoles, 19 marzo, 2008
Música de Windows
Melódica y friki canción realizada sólo con los sonidos del Windows XP.
Os deseo unas buenas vacaciones. ¡Hasta la próxima semana!
Fuente: El Blog de Dani
jueves, 28 febrero, 2008
Nunca puedes estar seguro
Viñeta 1: Tour de contabilidad. «Aquí tenemos nuestro generador de números aleatorios.»
Viñeta 2: «NUEVE NUEVE NUEVE NUEVE NUEVE NUEVE»
Viñeta 3: «¿Estás seguro que es aleatorio?» «Ése es el problema con la aleatoriedad: nunca puedes estar seguro.»
sábado, 23 febrero, 2008
El nacimiento de la mecánica cuántica
Cuando una teoría que intenta explicar la naturaleza comienza a dar resultados que no concuerdan con lo que medimos, ¡es un buen momento para cambiarla por otra nueva!
Esta es la historia de cómo un truco matemático significó en realidad una nueva interpretación de la realidad: el nacimiento de la mecánica cuántica. Y ocurrió a principios del siglo XX, momento en el que las dos teorías que intentaban explicar lo que nos rodea comenzaban a hacer aguas: la ley de gravitación universal y la teoría electromagnética clásica.
El problema del infinito
En el caso de la teoría electromagnética, el problema ocurría cuando se intentaba explicar la emisión de radiación de un objeto en equilibrio. Cualquier objeto emite una radiación que proviene de la vibración microscópica de las partículas que lo componen. Es la llamada radiación térmica.
Pues bien, usando las ecuaciones de la electrodinámica clásica, si calculabas la energía que emitía esta radiación térmica ¡daba infinito! Este ilógico resultado intrigaba a los físicos de la época.
El motivo por el que la energía de la radiación térmica de un objeto daba infinito, dicho de manera simple, provenía de que para calcularla debías sumar todas las frecuencias que emitía el objeto. Estas frecuencias, según la teoría electromagnética clásica, se distribuían de manera continua*, con lo que para sumarla debías hacerlo sobre todos los valores posibles: es decir, debías hacer una suma continua; una integral.
Entra Planck. Sale el electromagnetismo clásico.
Pero justo en el año 1900, a Max Planck se le ocurrió un truco matemático: se dio cuenta de que si sustituímos la integral por un sumatorio, es decir, por una suma no continua (discreta*), no sólo dejábamos de obtener un infinito, sino que además el resultado concordaba con lo que después medíamos.
Aceptar el truco matemático de Planck tenía serias implicaciones que chocaban con la teoría vigente: suponía aceptar que la energía y las frecuencias que emite cualquier objeto se distribuyen de manera discreta; es decir, están cuantizadas y sólo puede tener ciertos valores. Era realmente extraño y hasta el mismo Planck, cuando publicó los resultados, afirmaba que su hipótesis era, sin duda, falsa.
Sin embargo, el tiempo (y Niels Bohr, y Albert Einstein) demostró que no era así. Investigaciones posteriores pusieron de manifiesto no sólo que la energía estaba cuantizada, sino que a nivel microscópico muchas más cosas también lo están (como la misma luz, el momento lineal, las «órbitas» de los electrones en un átomo…). El problema es que en el mundo que vemos, el mundo macroscópico, no notamos esa cuantización por lo diminuta que es.
Tiempos distintos, mismos problemas
Lo que comenzó siendo un «truco matemático» tiene tantas implicaciones dentro de la física, que todavía, más de un siglo después, no logramos comprender muchas de ellas.
La teoría cuántica que surge con el descubrimiento de Planck ha evolucionado mucho. Ha llegado a lo que hoy llamamos Teoría Cuántica de Campos (TCC). Sin embargo, los problemas con los que nos encontramos ahora no han evolucionado tanto.
Y es que cuando en la TCC haces algunos cálculos básicos, te encuentras con que el resultado es, de nuevo, infinito. Y aunque existen trucos -bastante insulsos, por cierto- de esquivar esos infinitos, no terminamos de entender por qué los obtenemos ni cómo mejorar la teoría.
Para dar un poco de luz al tema se está construyendo una inmensa máquina en la frontera entre Suiza y Francia, el Large Hadron Collider, que esperamos que nos ayude a desvelar este gran misterio y a ampliar los límites del saber humano más allá de la TCC. Hasta el siguiente infinito…
——————–
* Una variable es continua si entre dos valores cualesquiera existen infinitos valores (como ocurre, por ejemplo, con los números reales). En contraposición, una variable es discreta cuando existen valores sucesivos que no tienen ninguno en medio de ellos (los números naturales N={0, 1, 2, 3, …} sería un ejemplo).
domingo, 27 enero, 2008
Entendiendo la entropía
La entropía puede parecer un concepto misterioso y difícil de entender, que comúnmente se relaciona con el desorden. Sin embargo, si nos adentramos en el significado de éste, no sólo veremos que se entiende fácilmente, sino que además encierra una serie de sutilezas que lo hacen muy interesante.
Antes de comenzar a explicar la entropía y ver qué relación real tiene ésta con el nivel de desorden, debemos hacer una pequeña y fácil introducción a la física estadística: diferenciar entre microestados y macroestados. ¡Pero no os asustéis! Aunque ahora hablaré de sistemas físicos como un gas en una botella y de magnitudes físicas como temperatura, volumen, etc. al final veremos de qué manera todo esto lo podremos extrapolar a cosas aún más cercanas.
Oxígeno en una botella
Pues bien, supongamos que tenemos un gas, por ejemplo oxígeno, dentro de una botella, a una temperatura de 25ºC. Como sabemos, los gases están compuestos por partículas más pequeñas, moléculas, que se van moviendo libremente ocupando todo el espacio en el que están encerrados (y si no están encerrados, expandiéndose indefinidamente). Esas partículas en movimiento estarán constantemente rebotando con las paredes de la botella y chocando entre sí. Además, cuanto mayor sea la temperatura, con más velocidad se moverán esas moléculas y con más fuerza chocarán contra las paredes de la botella -de hecho, lo que percibimos como temperatura es en realidad un movimiento microscópico de agitación de las moléculas-.
Lo interesante del caso, es que si pudiéramos tomar una serie de «fotos», cada una de las cuales captando la velocidad y posición de todas las moléculas para esta temperatura de la botella (25ºC), veríamos que éstas irían variando de una manera muy caótica en cada instantánea. Es decir, en la primera «foto» cada una de las moléculas tendrá una velocidad y una posición, y en la segunda, un segundo después, debido a la gran agitación de las moléculas, la velocidad y posición de cada una de ellas será muy diferente. Obtendríamos así millones de «fotos» distintas donde la posición y velocidad de cada una de las partículas, para la misma temperatura dada, serían muy diferentes (por supuesto, en la realidad no es posible tomar dichas fotos, pero si pudiéramos sabemos que éste sería el resultado).
Cada una de estas «fotos» es lo que llamamos un microestado. Es decir, la velocidad y posición de todas y cada una de la partícula en un instante con la botella a 25ºC es un microestado, que a su vez es diferente del microestado en un instante posterior para la misma temperatura de la botella. Por tanto, existe un conjunto de microestados para la temperatura de 25ºC, es decir, un conjunto de «fotos» posibles de la velocidad y posición de cada una de las partículas cuando la botella está a 25ºC.
Lo interesante del tema es que si, por ejemplo, aumentáramos la temperatura de la botella a 40ºC, las partículas se moverían con más velocidad, y el conjunto de microestados o «fotos» que obtendríamos sería diferente a cuando la teníamos a 25ºC.
Y aquí entra la definición del macroestado: es el estado que podemos medir con un simple termómetro (es decir, el estado macroscópico, estado físico, o simplemente, estado). En nuestro ejemplo, un macroestado sería la botella a una temperatura dada. Si cambiamos la temperatura, tendríamos un macroestado diferente.
Por tanto, y esto es muy importante, vemos que cada macroestado (es decir, cada temperatura de la botella) tiene asociado un conjunto diferente de microestados (es decir, una serie de posibilidades de posición y velocidad de todas las partículas).
Congelamos la botella
Metamos ahora la botella en un supercongelador donde bajamos su temperatura hasta -220ºC; haciendo así que el oxígeno se congele, se solidifique.
¿Qué ocurre en un sólido? Las partículas que lo componen ya no se mueven como en un gas, sino que están quietas siempre en la misma posición. Además, estas posiciones están más o menos definidas, es decir, una vez localizas un átomo de oxígeno, puedes saber aproximadamente donde estará el otro, pues en un sólido las partículas forman enlaces que las mantienen aproximadamente en su sitio. Por ello, podemos afirmar que un sólido está más ordenado que en un gas.
En el sólido, puesto que las partículas están quietas y más o menos ordenadas, el conjunto de velocidades y posiciones posibles será menor que en un gas. O, lo que es lo mismo, el número de microestados del oxígeno sólido en la botella es mucho menor que el número de microestados de un gas.
Un poco de matemáticas
Hemos visto que hay una relación entre el número de microestados y el orden. Cuantos más microestados tiene un macroestado, más desordenado está, porque más posiciones y velocidades distintas pueden tener sus partículas. Teniendo en cuenta esta relación entre microestados y macroestados, el genial físco Ludwig Boltzmann, a finales del siglo XIX, busca una magnitud física que dé cuenta del orden interno de un estado; y así define la entropía S de un macroestado como:
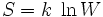
donde S es la entropía, k es un valor constante, y W es el número de estados.
¡Un momento! Dirá el lector menos acostumbrado a las fórmulas. ¿Qué significa esta ecuación? ¿Por qué decide Boltzmann que la entropía se defina así y no de otra manera?
La primera pregunta se resuelve fácilmente: lo que esta ecuación significa es que la entropía S de un estado físico crece con el número posible de microestados, W. La manera en la que S crece con W se ve muy bien en la siguiente gráfica:
La segunda cuestión es algo más técnica y simplemente diré que ésa es la única ecuación que cumple una serie de propiedades lógicas y necesarias.
Ropa tirada
Para ver mejor la relación entre la entropía y el orden, apliquemos lo aprendido a algo más cotidiano. Intuitivamente, ¿qué está más ordenado? ¿la ropa dentro del cajón o la ropa desperdigada por la habitación? El macroestado «ropa dentro del cajón» tiene mucho menos microestados posibles que el macroestado «ropa desperdigada por la habitación» por la sencilla razón de que fuera del cajón existen muchas más posiciones posibles de la ropa; es decir, existen muchos más microestados. Por tanto, podemos decir que «ropa fuera del cajón» tiene más entropía que «ropa dentro del cajón».
El desorden crece
En general, si quitamos restricciones a un sistema la entropía crece. Si no ponemos la ropa en el cajón y la vamos tirando por la habitación todo estará más desordenado. Si abrimos la botella de oxígeno a 25ºC el gas saldrá de la botella, expandiéndose, ocupando más espacio, y por ello aumentando el número de microestados posibles y su entropía. Si cogemos un saco de canicas y lo rasgamos todas las canicas caerán, desordenándose, aumentando sus posiciones posibles y aumentando la entropíá.
De hecho, hay una ley fundamental de la Naturaleza que dice que en todo proceso natural la entropía crece. Y ahora, que sabemos qué es la entropía, podemos decir que esto es así porque el número de microestados posibles es cada vez mayor.
¿Lo has entendido? ¡¡Pues a ordenar tu cuarto!!
PD: Esta anotación surge como consecuencia tardía y no gráfica de la petición que realiza Luis en su entretenido y creativo blog Entropía.
lunes, 29 octubre, 2007
martes, 23 octubre, 2007
¿Manchas solares?
Una foto del Sol, el astro rey. Podemos ver lo que parece una mancha solar…
…pero si aumentamos la imagen…
Ni más ni menos que ¡la Estación Espacial y el transbordador Atlantis!
Bella imagen. Clasificada como una de las diez mejores imágenes astronómicas de 2006.
Descubierto gracias a: Las penas del Agente Smith
sábado, 29 septiembre, 2007
850 x 77.1
Increible, pero cierto: ¿tenéis el Excel 97?
Si multiplicáis 850 x 77,1 el resultado que da es 100.000, cuando lo correcto es 65.535. Yo mismo he hecho la prueba y no salía de mi asombro.
Por lo visto es un error de la famosa hoja de «cálculo». ¿Qué ocurriría si una empresa tuviera un error financiero debido a esto? ¿Podría pedirle responsabilidades a Microsoft?
Leído en Microsiervos.
Por cierto, a modo de prueba e incluido en la barra lateral un nuevo apartado titulado «Mmm, interesante…» donde comparto aquellas entradas de otros blogs que leo y que creo que merecen la pena.
viernes, 21 septiembre, 2007
Distribución de visitas de Inquietudes
En el post sobre el record de visitas de Agosto, mi hermano Dani me hizo un inspirador comentario que me llevó a la siguiente pregunta: ¿cómo se distribuyen las visitas a lo largo de los posts de Inquietudes?
Con un poco de Excel y paciencia, obtuve la respuesta:
¿Qué significa esta gráfica? Aquí se representa el número de posts que tienen menos visitas que las indicadas en el eje X. Como se ve, el grueso de mis posts tienen entre 10 y 100 visitas. Es decir, el último punto arriba a la derecha, dice que hay 165 posts con menos de 14.000 visitas. Lo más sorprendente es que sólo 2 posts suman más visitas que los otros 163 restantes (¿adivináis cuáles?). De hecho, con sólo 16 posts (el 10%) cubro el 80% de las visitas.
Es importante conocer cuáles son los posts con más visitas de tu blog, pues la mayoría de éstas vienen de buscadores, y por tanto de gente que no lee frecuentemente tu blog. Si los tienes localizados, puedes usar estrategias de punto de entrada para “enganchar” a estos lectores a tu blog y así tener más lectores habituales.
Volviendo a la distribución, tengo curiosidad por saber qué aspecto tendrá la de los blogs más visitados, como Microsiervos o ALT1040. ¿Seguirán un patrón similar?
Inquietudes... 